Grundlagen Widerstände SMD und Bedrahtet
Widerstände – die allgegenwärtigsten elektronischen Bauelemente. Sie sind ein kritisches Stück in fast jedem Stromkreis. Und sie spielen eine wichtige Rolle in unserer Lieblingsgleichung, dem Ohmschen Gesetz.
Grundlagen von Widerständen
Widerstände sind elektronische Bauelemente, die einen spezifischen, unveränderlichen elektrischen Widerstand aufweisen. Der Widerstand des Bauteils begrenzt den Elektronenfluss durch eine Schaltung.
Sie sind passive Komponenten. Widerstände werden üblicherweise in Schaltungen eingesetzt, wo sie aktive Komponenten wie Operationsverstärker, Mikrocontroller und andere integrierte Schaltungen ergänzen. Üblicherweise werden Widerstände verwendet, um Strom zu begrenzen, Spannungen zu teilen und I/O-Leitungen auf GND oder die Versorgungsspannung zu ziehen.
Widerstandseinheiten
Der elektrische Widerstand eines Widerstandes wird in Ohm gemessen. Das Symbol für einen Ohm ist die griechische Großbuchstabe Omega: Ω. Die (etwas umständliche) Definition von 1 Ω ist der Widerstand zwischen zwei Punkten, mit einem Potential von 1 Volt (1 V) 1 Ampere (1 A) Strom fließt.
Je nach SI-Einheiten können größere oder kleinere Ohm-Werte mit einem Präfix wie kilo-, mega- oder giga- abgeglichen werden, um große Werte leichter lesbar zu machen. Es ist sehr verbreitet, Widerstände im Kilohm-Bereich (kΩ) und im Megaohm-Bereich (MΩ) anzugeben (viel weniger häufig sind Miliohm-Widerstände in (mΩ) angegeben). Zum Beispiel entspricht ein 4700 Ω-Widerstand einem 4,7 kΩ-Widerstand, und ein 5600000 Ω-Widerstand kann als 5600 kΩ oder (häufiger als) 5,6 MΩ geschrieben werden.
Schematisches Symbol / Schaltplansymbol
Alle Widerstände haben zwei Anschlüsse, einen Anschluss an jedem Ende des Widerstandes. Wenn ein Widerstand auf einem Schaltplan modelliert wird, wird er als eines dieser beiden Symbole angezeigt:
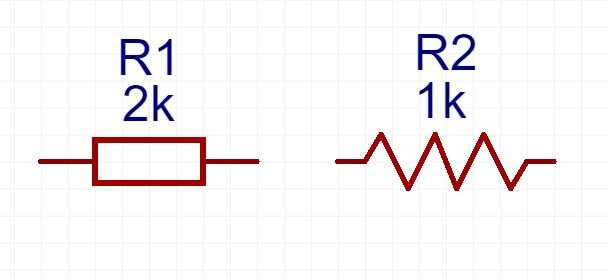 Zwei gängige Widerstands-Schaltbilder. R1 ist ein internationaler 2 kΩ-Widerstand und R2 ist ein amerikanischer 1 kΩ-Widerstand.
Zwei gängige Widerstands-Schaltbilder. R1 ist ein internationaler 2 kΩ-Widerstand und R2 ist ein amerikanischer 1 kΩ-Widerstand.Arten von Widerständen
Widerstände gibt es in einer Vielzahl von Formen und Größen. Es kann sich dabei um eine Bedrahtete- oder um eine SMD-Widerstände handeln.
Bedrahtete Widerstände haben lange, biegsame Leitungen, die in eine Lochrasterplatine eingesteckt oder von Hand in eine Prototypingplatine oder Leiterplatte (PCB) eingelötet werden können. Diese Widerstände sind in der Regel im Bereich des Breadboarding, Prototyping nützlich oder auf jeden Fall dort, wo man lieber keine winzigen, kleinen, 0,6 mm langen SMD-Widerstände löten möchte. Die langen Drähte erfordern in der Regel ein Kürzung.
Die gebräuchlichsten Durchgangswiderstände sind in einem axialen Gehäuse untergebracht. Die Größe eines Axialwiderstands ist abhängig von seiner Leistung. Ein gewöhnlicher 0,5 W-Widerstand misst etwa 9,2 mm, während ein kleinerer 0,25 W-Widerstand etwa 6,3 mm lang ist.
SMD Widerstände sind in der Regel winzige schwarze Rechtecke, die auf beiden Seiten mit noch kleineren, glänzenden, silbernen, leitfähigen Kanten abgeschlossen werden. Diese Widerstände sind für den Einsatz auf Leiterplatten vorgesehen, wo sie auf die entsprechenden Pads gelötet werden. Weil diese Widerstände so klein sind, werden sie in der Regel von Pick and Place Maschinen in Position gebracht und durch einen Ofen geschickt, wo das Lot schmilzt und sie an Ort und Stelle hält.
Eine Übersicht zu den SMD-Widerstandsgrößen ist hier hinterlegt.
Widerstandszusammensetzungen
Widerstände können aus einer Vielzahl von Materialien aufgebaut werden. Die gebräuchlichsten, modernen Widerstände bestehen entweder aus einem Kohlenstoff-, Metall- oder Metalloxidfilm.
Ablesen von Widerstandswerten
Axialwiderstände verwenden in der Regel Farbringe, um ihren Wert anzuzeigen. Die meisten dieser Widerstände haben vier Farbbänder, die den Widerstand umkreisen.
Die ersten beiden Bänder zeigen die beiden höchstwertigsten Stellen des Widerstandswertes an. Das dritte Band ist ein Gewichtswert, der die beiden höchstwertigen Stellen mit einer Zehnerpotenz multipliziert.
Der letzte Ring gibt die Toleranz des Widerstandes an. Die Toleranz gibt an, wie viel mehr oder weniger der tatsächliche Widerstandswert des Widerstandes bezogen auf den Nennwert aufweisen kann. Kein Widerstand wird in Perfektion gefertigt, und unterschiedliche Herstellungsverfahren führen zu besseren oder schlechteren Toleranzen. Zum Beispiel könnte ein 100 Ω-Widerstand mit 5 % Toleranz tatsächlich irgendwo zwischen 95 Ω und 105 Ω liegen.
Woran erkennt man, welcher Ring der erste und letzte ist? Der letzte, Toleranzring ist oft klar von den Wertringen getrennt, und normalerweise ist er entweder silbern oder golden.
Hier ist eine Tabelle der einzelnen Farben und welche Werte, Multiplikatoren oder Toleranzen sie repräsentieren:
| Farbe | Wert | Multiplikator | Toleranz |
|---|---|---|---|
| Schwarz | 0 | 1 | |
| Braun | 1 | 10 | |
| Rot | 2 | 100 | |
| Orange | 3 | 1000 | |
| Gelb | 4 | 10000 | |
| Grün | 5 | 100000 | |
| Blau | 6 | 1000000 | |
| Violet | 7 | 10000000 | |
| Grau | 8 | 100000000 | |
| Weiß | 9 | 1000000000 | |
| Gold | ±5 % | ||
| Silver | ±10 % |
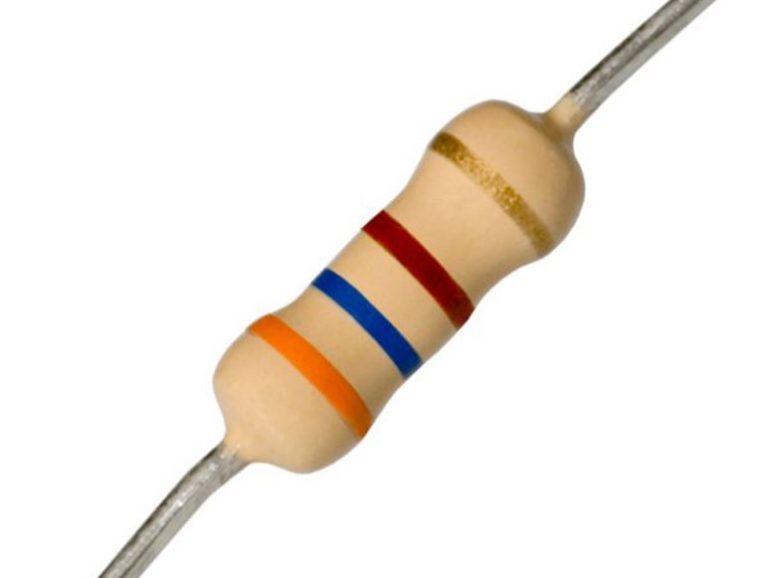
Hier ist ein Beispiel für einen 3,6 kΩ Widerstand mit vier Farbringen:
Wenn Sie die Farbringe der Widerstände dekodieren, konsultieren Sie eine Tabelle mit den Farbcodes der Widerstände, wie oben abgebildet. Suchen Sie für die ersten beiden Ringe nach dem Wert der entsprechenden Ziffer der Farbe. Der Widerstand 3,6 kΩ hat zu Beginn einen Orangen Ring gefolgt von Blau mit den Ziffern 3 und 6 (36). Der dritte Ring ist Rot, was bedeutet, dass die 36 mit 10² (oder 100) multipliziert werden sollte. 36 mal 100 ist 3600!
SMD-Widerstände, wie die in 0603- oder 0805-Gehäusen, haben ihre eigene Art, ihren Wert darzustellen. Es gibt ein paar gängige Markierungsmethoden, die Sie auf diesen Widerständen sehen werden. Normalerweise haben sie drei bis vier Zeichen – Zahlen oder Buchstaben – auf die Oberseite des Gehäuses aufgedruckt.
-
Dreistellige Markierung
Bei der 3-stelligen Markierung gibt es drei Ziffern. Die erste und zweite Ziffer zeigen die signifikanten Zahlen an, die dritte Ziffer ist der Multiplikator. Anstelle der Farbringe wird in Zahlen die tatsächliche Zahl verwendet. Wenn der SMD-Widerstand z.B. die Zahlen 472 hat, zeigt er 4, 7 = 47 x 10² Ohm an. Das entspricht dem Wert von 4,7 kΩ. Auch die Widerstände, welche als 100 markiert sind, sind keine 100 Ohm Widerstände, sondern 10×100 = 10 Ω oder 10×1 = 10 Ω. Bei Widerständen unter 10 Ohm wird der Buchstabe R an der Stelle der Dezimalstelle verwendet. Zum Beispiel repräsentiert 5R6 5,6 Ω.
3-stellige Beispiele:
- 220 = 22 × 100 (1) = 22 Ω (nicht 220 Ω!)
- 471 = 47 × 101 (10) = 470 Ω
- 102 = 10 × 102 (100) = 1000 Ω oder 1 kΩ
- 3R3 = 3,3 Ω
-
Vierstellige Markierung
4-stellige Markierungen kennzeichnen SMD-Widerstände mit hoher Toleranz. Bei diesen Widerständen stellen die erste, zweite und dritte Ziffer signifikante Werte dar, während die vierte Ziffer den Multiplikator darstellt. Zum Beispiel, wenn die Zahlen 4702 lautet, dann ist der Wert 470 x 10^2 Ohm oder 47 kΩ. Bei der 4-stelligen Kennzeichnung verwenden die Werte unter 100 Ohm den Buchstaben R an der Stelle des Dezimalpunktes.
4-stellige Beispiele:
- 4700 = 470 × 100 (1) = 470 Ω (nicht 4700Ω!)
- 2001 = 200 × 101 (10) = 2000 Ω oder 2 kΩ
- 1002 = 100 × 102 (100) = 10000 Ω oder 10 kΩ
- 15R0 = 15,0 Ω
- EIA 96 marking
Das Markierungssystem EIA 96 wird für Widerstände mit 1 % Toleranz verwendet. Bei dieser Kennzeichnung wird ein dreistelliger Code verwendet. Die ersten und zweiten Ziffern geben den Widerstandswert an und das dritte Zeichen ist ein Buchstabe, der den Multiplikator angibt.Dabei gibt es die folgenden Buchstaben: Z(0.001), Y oder R(0.01), X oder S(0.1), A(1), B oder H(10), C(100), D(1000), E(10,000), F(1,00000) etc.EIA-96 Beispiele:01Y = 100 × 0,01 = 1 Ω
68X = 499 × 0,1 = 49, 9 Ω
76X = 604 × 0,1 = 60,4 Ω
01A = 100 × 1 = 100 Ω
29B = 196 × 10 = 1,96 kΩ
01C = 100 × 100 = 10 kΩ -
Andere Markierungen an SMD Widerständen
- SMD-Widerstände mit einer Markierung von 0, 00, 000 oder 0000 sind Jumper oder Null-Ohm-Brücken.
- Der SMD-Widerstand, der mit dem standardmäßigen 3-stelligen Code und einem kurzen Balken unterhalb der Markierung gekennzeichnet ist, bezeichnet eine Genauigkeit von 1 % oder weniger.
- SMD-Widerstände in der Größenordnung von Milliohm, die für Strommessanwendungen vorgesehen sind, werden oft mit einem Buchstaben M oder m gekennzeichnet, der die Position des Dezimalpunkts angibt. Zum Beispiel: 1M50 = 1,50 mΩ
Leistungsbestimmung über einem Widerstand
Die Leistung wird in der Regel durch Multiplikation von Spannung und Strom ![]() berechnet. Aber durch die Anwendung des Ohmschen Gesetzes können wir den Widerstandswert auch für die Berechnung der Leistung verwenden. Wenn wir den Strom kennen, der durch einen Widerstand fließt, können wir die Leistung wie folgt berechnen:
berechnet. Aber durch die Anwendung des Ohmschen Gesetzes können wir den Widerstandswert auch für die Berechnung der Leistung verwenden. Wenn wir den Strom kennen, der durch einen Widerstand fließt, können wir die Leistung wie folgt berechnen:
![]()
Wenn wir den Spannungsabfall über einem Widerstand kennen, kann die Leistung wie folgt berechnet werden:
![]()
Reihen- und Parallelwiderstände
Widerstände werden in der Elektronik ständig miteinander gepaart, meist in Reihen- oder Parallelschaltung. Wenn Widerstände in Reihe oder parallel kombiniert werden, bilden sie einen Gesamtwiderstand, der mit einer von zwei Gleichungen berechnet werden kann. Das Wissen, wie Widerstandswerte kombiniert werden, ist nützlich, wenn Sie einen bestimmten Widerstandswert erstellen müssen.
Serienwiderstände
Bei Reihenschaltung addieren sich die Widerstandswerte einfach.
![]()
Wenn Sie also z.B. nur einen Widerstand von 12,47 kΩ benötigen, suchen Sie sich gebräuchliche Widerstandswerte von 12 kΩ und 470Ω aus und reihen diese in Serie zusammen.
Parallelwiderstände
Den Widerstand von parallelen Widerständen zu finden, ist nicht ganz so einfach. Der Gesamtwiderstand von ![]() parallel geschalteten Widerstände ist der Kehrwert der Summe aller Kehrwerte der parallelen Widerstände.
parallel geschalteten Widerstände ist der Kehrwert der Summe aller Kehrwerte der parallelen Widerstände.
![]()
Als Sonderfall dieser Gleichung: Wenn man nur zwei Widerstände parallel hat, kann man mit dieser weniger komplexen Gleichung ihren Gesamtwiderstand berechnen:
![]()
Als ein noch speziellerer Fall dieser Gleichung, wenn man zwei parallele Widerstände mit gleichem Wert hat, ist der Gesamtwiderstand die Hälfte ihres Wertes. Wenn z.B. zwei 10 kΩ Widerstände parallel geschaltet sind, beträgt ihr Gesamtwiderstand 5 kΩ.
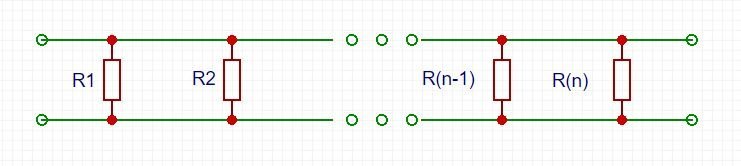
Widerstandsnetzwerke
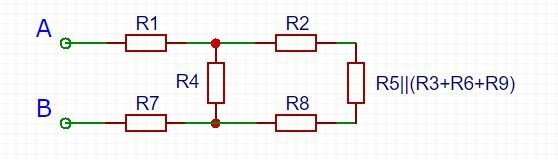
Die Kombination von parallelen und in Reihe verschalteten Widerständen führt zu Widerstandsnetzwerken. Meist beläuft es sich auf die Bestimmung des Gesamtwiderstandes zwischen zwei Punkten (![]() und
und ![]() ) im Schaltkreis.
) im Schaltkreis.
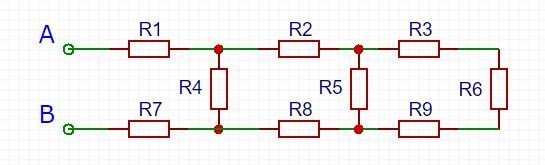
Um ein solches Problem zu lösen, beginnen Sie am hinteren Ende der Schaltung und vereinfachen in Richtung der beiden Punkte (![]() und
und ![]() ). In diesem Fall sind
). In diesem Fall sind ![]() ,
, ![]() und
und ![]() alle in Reihe geschaltet und können addiert werden. Diese drei Widerstände sind parallel zu
alle in Reihe geschaltet und können addiert werden. Diese drei Widerstände sind parallel zu ![]() , so dass diese vier Widerstände zu einem mit einem Widerstand von
, so dass diese vier Widerstände zu einem mit einem Widerstand von ![]() zusammengesetzt werden können. Wir erhalten somit:
zusammengesetzt werden können. Wir erhalten somit:
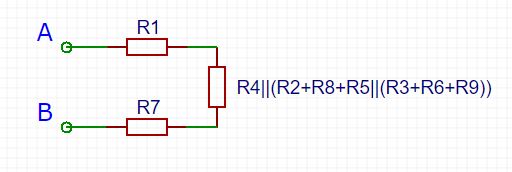
Die vier rechten Widerstände können nun noch weiter vereinfacht werden. ![]() ,
, ![]() und unser Konglomerat sind alle in Serie und können hinzugefügt werden. Dann sind diese Vorwiderstände alle parallel zu
und unser Konglomerat sind alle in Serie und können hinzugefügt werden. Dann sind diese Vorwiderstände alle parallel zu ![]() .
.
Und das sind nur noch drei Widerstände zwischen den Klemme ![]() und
und ![]() . Der Gesamtwiderstand dieser Schaltung ist also:
. Der Gesamtwiderstand dieser Schaltung ist also: ![]() .
.
Anwendungsbeispiele
Widerstände gibt es in fast jedem elektronischen Schaltkreis. Hier sind einige Beispiele für Schaltungen, die stark von Widerständen abhängen.
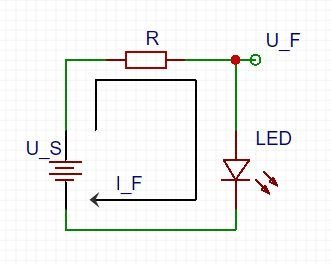
LED-Strombegrenzung (Vorwiderstand)
Widerstände sind der Hauptgrund, um sicherzustellen, dass die LEDs nicht durchbrennt, wenn die Stromversorgung eingeschaltet wird. Durch die Reihenschaltung eines Widerstandes mit einer LED kann der Strom, der durch die beiden Komponenten fließt, auf einen spezifizierten Wert begrenzt werden.
Achten Sie bei der Dimensionierung eines Strombegrenzungswiderstandes auf zwei charakteristische Werte der LED: die typische Durchlassspannung und den maximalen Durchlassstrom. Die typische Durchlassspannung ist die Spannung, die benötigt wird, um eine LED zum Leuchten zu bringen, und sie variiert (normalerweise zwischen 1,7 V und 3,4 V), je nach Farbe und Typ der LED. Der maximale Vorwärtsstrom liegt normalerweise bei 20 mA für gewöhnliche LEDs. Der Dauerstrom durch die LED sollte immer gleich oder kleiner als dieser Nennstrom sein.
Sobald Sie mit diese beiden Werte vertraut sind, können Sie mit dieser Gleichung einen Strombegrenzungswiderstand berechnen:
![]()
![]() ist die Quellspannung – in der Regel eine Batterie- oder Versorgungsspannung.
ist die Quellspannung – in der Regel eine Batterie- oder Versorgungsspannung. ![]() und
und ![]() sind die Vorwärtsspannung der LED und der gewünschte Strom, der durch die LED fließt.
sind die Vorwärtsspannung der LED und der gewünschte Strom, der durch die LED fließt.
Nehmen wir zum Beispiel an, Sie haben eine 9V-Batterie, um eine LED mit Strom zu versorgen. Wenn es sich um eine gewöhnliche rote LED handelt, könnte sie eine Durchlassspannung von ca. 1,8 V haben. Wenn Sie den Strom auf 10 mA begrenzen wollen, verwenden Sie einen Vorwiderstand von ca. 720Ω.
![]()
Spannungsteiler
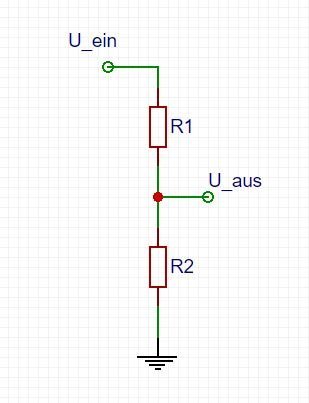
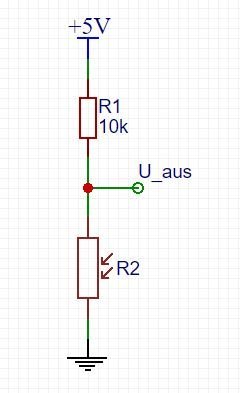
Ein Spannungsteiler ist eine Widerstandsschaltung, die eine große Ausgangsspannung in eine kleinere umwandelt. Mit nur zwei in Reihe geschalteten Widerständen kann eine Ausgangsspannung erzeugt werden, die einen Bruchteil der Eingangsspannung besitzt.
Hier ist die Spannungsteiler-Schaltung:
Zwei Widerstände, ![]() und
und ![]() , werden in Reihe geschaltet und eine Spannungsquelle
, werden in Reihe geschaltet und eine Spannungsquelle ![]() wird über diese geteilt. Die Spannung von
wird über diese geteilt. Die Spannung von ![]() nach
nach ![]() kann wie folgt berechnet werden:
kann wie folgt berechnet werden:
![]()
Wenn z.B. ![]() 1,7 kΩ und
1,7 kΩ und ![]() 3,3 kΩ wären, könnte eine 5 V Eingangsspannung an der
3,3 kΩ wären, könnte eine 5 V Eingangsspannung an der ![]() -Klemme in 3,3 V umgewandelt werden.
-Klemme in 3,3 V umgewandelt werden.
Spannungsteiler sind sehr praktisch zum auswerten von resistiven Sensoren, wie Fotozellen, Flex-Sensoren und druckempfindlichen Widerständen. Eine Hälfte des Spannungsteilers ist der Sensor und der andere Teil ist ein konstanter Widerstand. Die Ausgangsspannung zwischen den beiden Komponenten wird an einen Analog-Digital-Wandler auf einem Mikrocontroller (MCU) angeschlossen, um den Sensorwert auszulesen.
Pull-up / Pull-down Widerstände
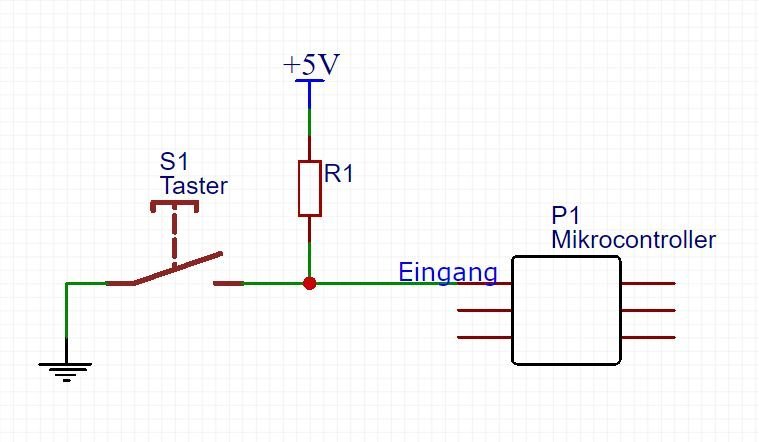
Ein Pull-Up-Widerstand wird verwendet, um den Eingangspin eines Mikrocontrollers in einen definierten Zustand zu bringen. Ein Ende des Widerstandes ist mit dem Pin des Mikrocontrollers verbunden, das andere Ende wird mit der Versorgungsspannung (üblicherweise 5 V oder 3,3 V) verbunden.
Ohne Pull-Up-Widerstand könnten die Eingänge des Mikrocontrollers potentialfrei bleiben. Es gibt keinen definierten zustand.
Pull-Up-Widerstände werden häufig verwendet, wenn digitale Eingänge mit einem Taster- oder Schalteingang verbunden werden. Der Pull-Up-Widerstand kann bei geöffnetem Schalter den Eingangs-Pin auf das Niveau der Versorgungsspannung ziehen. Und er schützt den Stromkreis vor einem Kurzschluss, wenn der Schalter geschlossen ist.
In der obigen Schaltung ist der Eingangspin des Mikrocontrollers bei geöffnetem Schalter über den Pull-up-Widerstand mit 5 V verbunden. Beim Schließen des Schalters wird der Eingangspin direkt mit GND verbunden.
Der Wert eines Pull-Up-Widerstandes muss in der Regel nicht berechnet werden. Aber er sollte hoch genug sein, dass nicht zu viel Leistung verloren geht, wenn man 5 V mit GND über den Widerstand verbindet. Normalerweise funktionieren Werte um 10 kΩ gut.
Links zu verwaten Themen




Noch keine Kommentare.